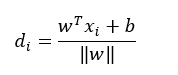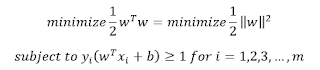SUPPORT VECTOR MACHINES IN MACHINE LEARNING/PYTHON/ARTIFICIAL INTELLIGENCE

Support vector machine

• Types of Support Vector Machines
• Working on Support Vector Machine
• Support Vector Machine Terminology
• Mathematical Intuition of Support Vector Machine
• Popular Kernel Functions in SVM
• Advantages of Support Vector Machine
• Disadvantages of Support Vector Machine 

Support Vector Machine algorithms (SVMs) are a notable class of supervised learning models and techniques for regression and classification. Fundamentally, support vector machines (SVMs) are discriminative classifiers; they identify the optimal hyperplane through feature space optimization. This hyperplane is used to distinguish different groups of data points. Regression analysis, outlier detection, and a range of classification issues, both linear and nonlinear, can all be handled using support vector machines (SVMs), which are effective and incredibly adaptable.

These methods find applications in numerous fields, including handwriting identification, spam detection, text categorization, gene classification, and many more. Support vector machines (SVMs) are highly effective at handling multidimensional data with nonlinear correlations.

The primary goal of support vector machines (SVMs) is to locate the feature space hyperplane that maximizes the margin between the nearest data points from various classes. The hyperplane's dimensionality is proportional to the dataset's feature count. A hyperplane, for instance, is only a straight line in the case of two features. It becomes a plane once three properties are added. As the number of qualities increases, the hyperplane fills a higher-dimensional space, making it more challenging to comprehend and portray. SVM machine learning Python is very easy to understand therefore we study with the help of Python in this blog. In this model, we learn about the SVM algorithm and explain the support vector machine.

Example of Support Vector Machine

Let’s suppose we are farmers and we are sorting grains. Normally we would use a sieve, for sorting the grains, but what if the grains are oddly shaped or similar in size? In such type of situation, a Support Vector Machine (SVM) can be used or acts like a smart sorting machine.

SVM machine learning excels in classification-like tasks, like separating the wheat from the chaff (that bad vs good grains). It can also analyze the data points (wheat grains) based on their features like size, color, weight, etc. Let’s take grain size and texture as a feature for our case.

With the help of the SVM algorithm in machine learning, we create a separation line or hyperplane, in this feature space. This hyperplane or separation line strategically maximizes the distance between the two categories, wheat and chaff. Grains (data points) on one side of the line are classified as wheat, and points which are on the other side of the line are classified as chaff.

The key advantage of SVM model machine learning is finding the best separation line, even if the data isn’t perfectly linear. Let's suppose we have some grains that are oddly shaped and categorized as outliers. SVM can handle these by finding the best possible hyperplane even with such complexities.

Once the SVM is trained on the labeled data (wheat and chaff samples), then the SVM can classify new grains (data points) that it still doesn’t see. The SVM analyzes the features of these new grains and then assigns them into one class based on their position relative to the hyperplane.

Types of Support Vector Machines

We can divide the Support Vector Machines into 2 categories:

Linear Support Vector Machines (SVM) use datasets with linear separability, meaning that classes can be effectively discriminated using a single straight line. This is the typical result when the data points are neatly divided into two classes by a linear border. If this is the case, we build the most efficient decision border between the classes using linear support vector machine classifiers.

In contrast, non-linear support vector machines (SVM) are used when a straight line cannot be used to separate the non-linear data. Because of the way the data points are arranged, a more complex, non-linear decision boundary could be needed in certain situations to split the classes appropriately. Such non-linear data is handled by a Non-linear Support Vector Machine (SVM) classifier. These classifiers may handle data with non-linear correlations by converting the data into a higher-dimensional space where linear separation is possible using techniques like kernel functions.

How does Support Vector Machine work?

Linear SVM - One of the reasonable choices for the best hyperplane is the one that has the largest separation or margin between the two classes.

Image source original

The optimal hyperplane was determined by measuring the length of time a line is separated from the closest data point on either side. This specific type of hyperplane is called a "maximum-margin hyperplane or hard margin". Now all we have to do is select line L2 from the above figure. Let’s consider another scenario which is shown in the below image.

Image source original

In the image above, when there is just one blue dot in the red area, how do support vector machines (SVMs) operate? To handle this kind of data, the SVM establishes the maximum margin in the same way that it did for the prior data set. It then has to add a penalty each time a point goes over the margin. These kinds of circumstances are referred to as "soft margins".  Whenever the soft margin appears in the dataset, the SVM applies the formula (1/margin+Λ(∑Penalty)) in an attempt to reduce it. Hinge loss is mostly used to apply the penalty. If there is no violation, the loss is directly correlated with the violation's distance.

Non-linear SVM-   Till now we have looked only the linear SVM or linearly separable data, now we look at datasets that are not linearly separable. This type of data cannot be separated by a single straight line. Below is the image of such a type dataset.

Image source original 

By looking at the above diagram we can conclude that we cannot clearly separate the data points using a single line. Also if we have more than two classes it is impossible to separate them using a single straight line. In the above diagram, we can see that a single line cannot separate them but a circular hyperplane can separate the two classes. Therefore, we can add another coordinate Z, which gets help from X and Y in which Z = X² + Y². By adding a third dimension the graph can change into: -

Image source original

Because the above diagram tries to show 3-D space it looks like a parallel to the x-axis separates them. If we convert it into 2D space where Z = 1, then it can look like the below image:

Image source original

In the above diagram we can see that the dataset is separated with the help of Z coordinate where Z = 1, therefore, we get a circumference of radius 1 in the above case.

Support Vector Machine Terminology

A hyperplane serves as the decision boundary and partitions the feature space into multiple classes in Support Vector Machines (SVM). For linearly separable datasets, the hyperplane is represented by a linear equation, which is typically expressed as wx + b = 0. The variables 'w', 'x', and 'b' in this equation represent the weights, input characteristics, and bias term, respectively.

Support vectors or the data points closest to the hyperplane, are essential for determining the hyperplane and margin. The margin is the length of the support vector machines that separates them from the hyperplane. Optimizing the margin is a crucial goal of support vector machines (SVM) since a larger margin typically leads to better classification performance.

Support vector machines (SVMs) convert the input data points into a feature space with additional dimensions by using mathematical functions known as kernel functions. It is feasible to discover nonlinear decision boundaries with this adjustment even in cases where the data points aren't linearly separable in their original input space. It is often preferable to use kernels that use sigmoid, linear, polynomial, or radial basis functions (RBFs).

Support vector machines employ two types of margins: firm and soft. A hard margin hyperplane flawlessly separates the data points of various categories without misclassifications, in contrast to a soft margin hyperplane, which allows for certain violations or misclassifications—usually added to deal with outliers or incomplete separability.

In SVM, the regularization value 'C' guarantees a balance between margin optimization and misclassification penalty minimization. A larger 'C' value translates into a harsher penalty, which implies fewer misclassifications and a narrower margin.

Hinge loss is a popular loss function in support vector machines (SVMs) that is used to penalize margin violations or overclassification. SVM objective functions often include a hinge loss component along with a regularization term.

The dual problem in support vector machines (SVM) is to optimize the Lagrange multipliers associated with the support vectors. This formulation allows the use of kernel methods, resulting in more efficient computation, especially in high-dimensional environments.

Mathematical intuition of Support Vector Machine

Assume we are given a binary classification task with two labels: +1 and -1. The training dataset has X features and Y labels. For this reason, the linear hyperplane's equation can be written as:

The vector W in this case denotes the normal of the hyperplane. The axis that crosses the hyperplane is this one. In addition to the normal vector w, the hyperplane's offset from the origin is represented by the equation's parameter b.

The distance between a data point let x_i and the decision boundary can be calculated as:

Here ||w|| is the Euclidean norm of the weight vector w.

For Linear SVM classifier:

Optimization

For hard margin linear SVM classifier:

In the above equation, the target variable or label for the ith training instance is represented by the symbol ti. Ti=-1 denotes the negative occurrence (yi = 0), and Ti=1 denotes the positive occurrence (yi = 1). If we are to move forward, the decision boundary needs to match the constraint: 

For soft margin linear SVM classifier:

Dual Problem: To solve problems with support vector machines (SVMs), one must first determine which Lagrange multipliers correspond to which support vectors. We refer to this optimization issue as a dual problem. The optimal Lagrange multipliers α(i) optimize this dual objective function:

In above equation

• α_i (alpha subscript i)is the Lagrange multiplier which is associated with the ith training sample.
• K(x_i x_j ) (x subscript i and j) is the kernel function that computes the similarity between two samples x_i and x_j. They allow the SVM to handle nonlinear classification problems by implicitly mapping the samples with the higher-dimensional feature space.
• ∑α_i  represents the sum of all the Lagrange multipliers

Using the support of the vectors and the optimal Lagrange multipliers, the decision boundary of the support vector machines may be characterized once the dual issue has been solved. The decision boundary is provided by the support vectors, which are those in the training set with an i higher than 0:

Popular kernel functions in SVM

By converting low-dimensional input space into higher-dimensional space, support vector machines' kernels enable them to solve separable problems that were previously thought to be non-separable. It is quite helpful for problems involving non-linear separation. All we need to do is introduce the kernel and figure out how to partition the data according to the labels or outputs it defines. The kernel does extremely complex data manipulations:

Advantages of Support Vector Machine

• It is effective with high-dimensional data or cases.
• Because it uses a decision function known as support vectors memory is efficient for the training of subsets.
• We can use different kernel functions for the decision functions and it is also possible to specify the custom kernels.

Disadvantages of Support Vector Machine

• Big data sets aren't a good fit for the Support Vector Machine method.
• When dealing with large datasets, the Support Vector Machine technique doesn't work well.
• Support Vector Machine is ineffective when applied to a very big dataset.

Application of support vector machine

Many different types of businesses use Support Vector Machine (SVM), a versatile machine learning method, to solve regression and classification issues. Using the feature space, SVM determines the optimum hyperplane that divides the classes best, maximizing the margin between them. This space improves the ability to generalize to new data and ensures that the model can withstand noise. In high-dimensional domains or situations with more attributes than samples, SVMs perform exceptionally well. By projecting the initial feature space into a higher-dimensional space, where classes are more easily distinguished, kernel functions enhance their ability to deal with non-linear data. Multiple fields make use of support vector machines (SVMs), such as biology, image recognition, text classification, and finance. Classification of texts makes use of support vector machines (SVMs) for applications such as document classification, sentiment analysis, and spam detection. Support vector machines (SVMs) find use in object detection, face recognition, and medical image analysis within the field of image recognition. Protein structure prediction, gene expression analysis, and drug discovery are some of the bioinformatics applications of support vector machines (SVMs). Financial institutions rely on support vector machines (SVMs) for a variety of tasks, including stock price forecasting, credit scoring, and loss prevention. With their robust and efficient solutions, SVMs improve data analysis and decision-making across many industries.

      Summary

    Support Vector Machines (SVM) serve as versatile algorithms employed across classification, regression, and outlier detection tasks. Their primary objective involves identifying the optimal hyperplane that effectively segregates different classes in a dataset by maximizing the margin between them. Operating within high-dimensional spaces, SVMs leverage diverse kernel functions to handle intricate data patterns and nonlinear relationships effectively. While SVMs offer robust performance, it's essential to acknowledge that they can pose computational challenges and demand meticulous parameter selection to achieve optimal results.

     Python Code

    Below we define support vector machine in Python code: - 

LOGISTIC REGRESSION IN MACHINE LEARNING/PYTHON/ARTIFICIAL INTELLIGENCE

Logistic Regression

• Types and terminologies of Logistic Regression
• Working of Logistic Regression
• Steps in Logistic Regression Modelling
• Logistic Regression Model Thresholding

Logistic regression machine learning, one of the most significant supervised machine learning algorithms, is typically applied to classification tasks. Finding the likelihood that an observation belongs to a certain class is the aim of classification problems, as opposed to continuous-outcome regression models. Logistic regression gets its name from the mathematical procedure that uses a sigmoid function to analyze the output of a linear regression function. The likelihood that an observation falls into a certain class is indicated by the probabilities that emerge from this transformation. In this blog, we learn logistic regression in Python.

Using a set of independent factors, logistic regression aims to forecast the categorical dependent variable. Logistic regression provides probabilistic numbers between 0 and 1, which indicate the likelihood that an observation belongs to a particular class, as opposed to exact categorical findings.

Although they are not the same, logistic regression and linear regression are comparable technically. They are both useful, nonetheless, despite this. Linear regression is used to handle issues with continuous value predictions, whereas logistic regression is better suited for classification tasks. Logistic regression fits the dataset with a logistic function, resulting in a curved 'S' form, to estimate the maximum output between 0 and 1. Identifying cancerous cells or a dog in an image are two instances of the kinds of data that this curve could be used to represent.

Logistic regression holds significant value in machine learning because it can effectively classify fresh data from both continuous and discrete datasets and generate probabilistic results. Observation categorization using several data sources is facilitated by this flexible and significant tool, which also helps identify the most influential variables for classification tasks. It is particularly useful in predictive modeling and decision-making processes. 

Image source original 

Logistic Function (Sigmoid Function)

In logistic regression, the determination of whether an observation belongs to a certain class relies on a threshold value, often set using the sigmoid function. Typically, a threshold of 0.5 is used for binary classification. Predicted value is placed in class 0 if it is less than 0.5; class 1 if it is more than or equal to 0.5. As a mathematical instrument, the sigmoid function maps expected values onto probabilities, hence converting real values into a range between 0 and 1.

This transformation is crucial in logistic regression, as the output must stay within the bounds of 0 and 1. The sigmoid function, often visualized as an 'S' curve, accomplishes this task by ensuring that predictions are constrained within these limits.

In logistic regression, certain prerequisites must be met. Firstly, the dependent variable must be categorical in nature, as logistic regression is specifically designed for classification tasks. Additionally, multicollinearity among independent variables should be avoided, as it can lead to instability in model estimates and complicate the interpretation of coefficients. By adhering to these requirements, logistic regression can effectively classify observations and provide valuable insights into categorical outcomes.

Types of Logistic Regression

Three different types of logistic regression can be distinguished:

There is a unique type of logistic regression that is known as binomial logistic regression. It has only two possible outcomes: true or false, pass or fail, etc.

Multinomial: In multinomial logistic regression it can have 3 or more than 3 outcomes it can also be in unordered manner.

Three or more outcomes can also be included in an ordinal category logistic regression; however, in this instance, the dependent variables are ranked from low to high.

Logistic Regression Example

We all get spammy emails even sometimes we get bombarded by them, but between these spammy emails, we get some important emails. To overcome such problems, we want a solution that can filter spammy emails from important emails. To achieve this, we want to train a model that automatically does this.

In such situations, logistic regression can help. The logistic regression algorithm can analyze the features of an email and predict the probability of whether the mail is spammy (dependent variable) or not. 

Some features can be in spam emails like

• Presence of spammy words (e.g., “FREE”, “URGENT” “4U”)
• Sender’s email address (unknown or known contact)
• Inclusion of attachments or links

To train our logistic regression model we collect a bunch of emails these emails include spammy and non-spammy emails. Then we labeled them accordingly after that we fed these labeled data to the logistic regression model. After receiving the data, the model tries to learn the pattern from it and tries to learn to differentiate spammy emails from normal emails.

 After learning from the data, the logistic regression does not just only answer yes or no, it also provides the probability between 0 (definitely not spam) and 1 (definitely spam). This probability allows us to set a threshold value. For example, if we set a threshold value of 0.6 as a spam threshold, then any email that has a probability over 0.6 is flagged as spam.

The beauty of this algorithm is that we can set the threshold value to our needs. If we want then we can even set the threshold value higher if we don’t want to miss any important email which might be flagged as spam. Inversely if we are less worried about missing important emails then we can set the threshold value lower.

Here we learn about logistic regression machine learning example in real-world situations.

Terminologies involved in Logistic Regression

The following terminology must be understood to completely understand how logistic regression operates:

The independent variables are the attributes, features, or qualities of the input that are used to predict the outcomes of the dependent variable.

The dependent variable, also known as the target variable, has values that the logistic regression model predicts or estimates.

A formula that illustrates the relationship between two variables—one of which is independent and the other dependent—is called a logistic function. Through the conversion of input variables, the logistic function generates probability values between zero and one.

The likelihood that an event will occur is directly correlated with its likelihood of not occurring. It presents an alternative perspective on probability.

The log-odds, sometimes referred to as the logit function, is the natural logarithm of the chances. A linear combination of intercepts and independent variables that describe the log probability of the dependent variable can be used to create a logistic regression model.

The estimated parameters of a logistic regression model, like a coefficient, reveal the type of relationship that exists between the two sets of data. They quantify the impact of independent influences on the likelihood of the result.

The log chances of setting each independent variable to zero are the intercept which is a constant feature of logistic regression models.

The logistic regression model's coefficients can be predicted or estimated by using maximum likelihood estimation. Finding the coefficients that maximize the chance of witnessing the data given the assumptions and structure of the model is the aim.

How does Logistic Regression work

Logistic regression modeling converts the continuous output of the linear regression function into values that may be categorized by using the sigmoid function. This mathematical function, commonly known as the logistic function, is crucial in transforming the set of real-valued independent variables into a binary range of 0 and 1.

The continuous output of the linear regression model is transformed into probabilities using logistic regression and the sigmoid function. These probabilities specifically indicate the likelihood that an observation falls into a particular category. This process aids in the classification of data into discrete categories by efficiently employing the input variables to anticipate categorical outputs.

Let us have independent input features in the below format cap

In this, the dependent variable Y only has binary values that are 0 and 1.

After that, we can apply the multi-linear function to the input features or variables X 

The weight or coefficient in this case is denoted by w_i=[w_1,w_2,w_3,…,w_m] (w subscript 1, 2,3 and m), the X-observation is represented by x_i, the bias factor—also known as the intercept—is represented by b. The preceding equation can instead be expressed as the bias and weight dot product.

Sigmoid Function

After that let's discuss the use of the sigmoid function in this the input will be z and we need to find the probability between 0 and 1 which is predicted by y.

Image Source original

As can be seen in the following picture, the sigmoid function converts the data from the continuous variables into a probability value between zero and one. As z gets closer to infinity, the value of σ(z) approaches 1, while as z gets closer to negative infinity, it approaches 0.0, and 1 is intrinsically linked in σ(z).

In the probability of being a class can be measured as:

Logistic Regression Equation

In logistic regression, there is a chance that something occurs or something does not occur, which is different from probability as probability is the ratio of something that possibly occurs with everything. So, it can be written as 

In this, we apply the log on the odd which makes it 

 The final equation or formula of logistic regression will be: 

Assumptions for Logistic Regression

The assumptions for logistic regression are as follows:

Independent observations – it means that every independent feature is independent from other features which leads to no correlation between them.

In logistic regression, certain conditions must be met for the model to perform effectively:

Binary dependent variables: The dependent variable in logistic regression should only be able to take on binary or dichotomous values. If there are multiple categories, the softmax function is utilized instead. This binary nature allows logistic regression to classify observations into two distinct groups based on the given input variables.

Log odds about independent factors: A dependent variable's log odds ought to be squared about the independent variables. This linear association ensures that changes in the independent variables correspond to proportional changes in the log odds of the outcome, facilitating accurate predictions.

No outliers: This relationship can be expressed correctly using the square of the log odds of a dependent variable about the independent factors. Therefore, it is important to address outliers or ensure they are not present in the dataset to maintain the model's accuracy and reliability.

Large sample size – for training machine learning algorithms we need to have a large dataset because it takes a lot of data to learn machine learning properly.

Applying steps in logistics regression modeling

If we want to utilize logistic regression properly for prediction, we need to follow the following structured approach:

Define the problem: At the start, we need to define the dependent variable and independent variables. Determining whether the problem involves binary classification or not is crucial.

Preprocessing and cleansing of the data is necessary after the problem has been determined. This includes ensuring the dataset functions well with logistic regression analysis, encoding categorical variables, and managing missing values.

Exploratory data analysis (EDA): By doing EDA, one may learn more about the dataset. While spotting unusual events guarantees data integrity, visualizing connections between dependent and independent variables helps to better comprehend the data.

Feature selection: Selecting relevant actual variables is vital for effective modeling. Features with significant relationships to the dependent variable are retained, while redundant or irrelevant features are removed to improve model performance.

Building a logistic regression model using the chosen real variables and estimating its coefficients using the training data.

Performance of the model is evaluated using AUC-ROC, F1-score, recall, accuracy, precision, and other measures. This makes the prediction accuracy of the model on new data evaluable.

Model improvement: Fine-tuning the model may be necessary to enhance its performance. Adding new features, utilizing regularization techniques, or adjusting independent variables can all improve the quality of your model and lower the risk of overfitting.

Model deployment: after we’re happy with the models’ result, it is ready for deployment in real-world scenarios. The model we get after training is then used to make predictions on new, unseen data, offering valuable insights for decision-making purposes.

Logistic Regression Model Thresholding

The logistics regression only becomes a classification technique because the threshold is brought to it. In logistics regression setting the threshold value is very important. The classification problem somehow depends on it quite much.

The recall and precision values very much affect the threshold value, we want both precision and recall to be one, but it is very difficult or even impossible for a good machine learning model so we want the value to come as much as possible close to one.

For deciding the precision-recall tradeoff (because when one increases another decreases), we can use the following arguments which can help to decide the threshold:

To attain a scenario of low precision and high recall, the focus lies on minimizing the number of false negatives while allowing a potentially higher number of false positives. This means selecting a decision threshold that prioritizes recall over precision. By doing so, the aim is to capture as many true positives as possible, even if it results in a relatively higher number of false positives.

Conversely, achieving high precision and low recall involves reducing the number of false positives while potentially accepting a higher number of false negatives. This entails choosing a decision threshold that emphasizes precision over recall. The goal is to ensure that the majority of the predicted positives are indeed true positives, even if it means sacrificing the ability to capture all actual positives, leading to a lower recall value.

Summary

Like linear regression logistic regression is also a very simple and easy-to-implement machine learning algorithm, it is used for classification problems where we need to check or select whether a thing belongs to one class or not. It has also a similar type of limitation as linear regression it also needs to be that there should be a linear relationship to exist in the independent and dependent variables and also it should have dependent data that can be used for classification purposes. In this chapter, we also learn about advanced logistic regression.

Python Code

Below is the logistic regression Python example code: -