K-MEANS CLUSTERING IN MACHINE LEARNING/PYTHON/ARTIFICIAL INTELLIGENCE

K-means Clustering

• Unsupervised Machine Learning
• K-Means Algorithm Working
• Choosing the Value of "K" in K-Means
• Advantages of K-Means Clustering
• Disadvantages of K-Means Clustering

Unsupervised machine learning is the autonomous pattern identification within unlabeled data by computers. This method avoids the machine learning using already labeled data. Its task is to organize unstructured data, detecting patterns, relationships, and variations independently. Various algorithms are employed for this purpose, with one such algorithm being K-Means clustering in machine learning.

One kind of unsupervised learning approach called K-Means clustering is intended to divide unlabeled datasets into discrete clusters. 'K' is the number of clusters the method seeks to find. For example, setting K=2 results in two clusters, while K=3 yields three clusters, and so on. Through iterative steps, the algorithm assigns data points to K clusters based on their similarities, ensuring each point belongs to a distinct cluster with similar characteristics. We apply k means clustering for customer segmentation because in customer segmentation using k means clustering, it becomes easier to work and understand.

As a centroid-oriented method, K-Means assigns a centroid to each cluster to minimize the total distance between data points and their corresponding clusters. An unlabeled dataset is first split into K clusters according to how similar the data points are to one another. Through iterative refinement, the algorithm adjusts the centroids until optimal clusters are achieved, with the specified value of K dictating the number of clusters formed.

Real-world example for k-means clustering

Let’s take a real-world example, there is a farmer’s market. However, as the market grew, it became more disorganized, making it difficult for vendors and customers to navigate. To end this problem the mayor of the village takes help from a data scientist Emily.

Emily started her work by meticulously gathering data on the products sold at the market, noting down details such as type, color, and price. After gaining these pieces of information, she apply k-means clustering algorithm to group similar products. Fruits, vegetables, grains, dairy products, and more began to form distinct clusters, creating a structured organization within the market.

After the clusters were identified the Mayor and Emily collaborated to redesign the layout of the market. They arranged vendor stalls according to the clusters, creating designed zones for each product category. Signs and labels were added to guide customers, ensuring a seamless shopping experience. They also use k means clustering for customer segmentation.

The k-means clustering algorithm mainly does two tasks:

• The iterative process of K-Means involves determining the optimal number of centroids or K center points. Through this iterative approach, the algorithm refines the value of K by evaluating various cluster configurations until an optimal solution is found.
• The K-Means algorithm assigns each data point to the nearest centroid or k-center. This process results in the formation of clusters where data points that are closest to a particular centroid are grouped together.

Therefore, similar data points belong to the same cluster and away from different data points or clusters.

Image source original

To calculate the similarity the algorithm will use the Euclidean distance as a measurement. The algorithm works as follows:

• Initially, the K-Means algorithm randomly selects k points from the dataset, designating them as means or cluster centroids.
• Subsequently, each item in the dataset is assigned to the nearest mean, grouping them into clusters. Following this, the means' coordinates are updated to the averages of all items within their respective clusters.
• The process iterates for a specified number of iterations, continuously refining the clusters with each iteration until convergence is achieved. At the end of the iterations, the algorithm produces the final clusters based on the updated means and the assignment of data points to their nearest centroids.

In this scenario, the term "points" representing means denotes the average value of the items grouped within the clusters. There are various methods to initialize these means. One method involves randomly selecting items from the dataset to serve as initial means. Another approach is to randomly generate mean values within the range of the dataset's boundaries as the starting points.

Here is the pseudocode of the K-means clustering algorithm:

Initialize k means with random values

• For a given number of iterations:
• Iterate through items:
• Find the mean closest to the item by calculating the Euclidean distance of the item with each of the means
• Assign item to mean
• Update mean by shifting it to the average of the items in that cluster

How K-Means algorithm work?

Let’s look at the steps of the k-means algorithm in machine learning and in general

Step 1 – Determine the appropriate value for K, which indicates the desired number of clusters to be created.

Step 2 – Choose K random points or centroids as the initial cluster centers, which may or may not be selected from the input dataset.

Step 3 – Assign each data point to the centroid that is closest to it, thereby grouping the points into K predefined clusters.

Step 4 – Compute the variance within each cluster and position a new centroid at the center of each cluster based on the calculated variance.

Step 5 – Proceed to the third stage iteratively, assigning each data point, using the revised centroids, to the closest centroid of the matching cluster.

Step 6 – If throughout the iteration any data points are moved to other centroids, the algorithm goes back to step 4 to recalculate the centroids. In any other case, it goes on to the last phase.

Step 7 –  After doing all of the above steps now we can say that our model is ready.

We can easily write the above clustering algorithm in Python.

Let’s understand the algorithm using images:

Let us have two variables n1 and n2. The x-y axis of the scatter plot of these two variables is shown below image:

Image source original

Now, to create a specified number 'k' of clusters (e.g., if k=2, then two clusters are to be formed), we proceed by selecting 'k' random points or centroids that will establish these clusters. These points can either be existing data points from the dataset or any arbitrary points. In the illustration below, two points have been randomly chosen as the 'k' points; it's important to note that these points, as shown in the image, are not part of the dataset's data points.

Image source original

It is now necessary to designate each point on the scatter plot to its nearest centroid or K-point. The process involves using mathematical formulas to determine the separation between two spots, thus we must draw a median between their centroids. displayed in the picture below.

Image source original

Data points on the left side of the line are closer to the K1 or cyan centroid, while those on the right side are closer to the violate centroid, as can be seen in the below image.

Image source original

We must choose "a new centroid" and repeat the process to locate the closest cluster. The centroids' center of gravity was used to choose the new centroids, which are displayed in the image below:

Image source original

All of the data points must be moved to the centroid nearest to them as part of the process. This necessitates recalculating the median line. After that, as can be seen below, the image displays the updated data point distribution:

Image source original

In the image above, it's noticeable that one violate point is situated above the median line, placing it on the side associated with the cyan centroid. Similarly, some cyan points are positioned on the side attributed to the violated centroid. Consequently, these points necessitate reassignment to the appropriate new centroids.

Image source original

Following the reassignment observed in the depicted image, the algorithm progresses back to the step involving the determination of new centroids or K-points.

The iterative process continues as the algorithm recalculates the center of gravity for the centroids, resulting in new centroids depicted in the image below:

Image source original

Once the new centroids are determined, the algorithm redraws the median line and reassigns the data points accordingly. This process alters the visualization of the data points, as illustrated in the following image:

Image source original

The diagram above demonstrates that each data point is correctly assigned to its respective cluster, with no dissimilar points appearing on opposite sides of the line. This outcome signifies the successful formation of our model.

Image source original

With our model now complete, we can remove the assumed centroids, revealing the final clusters as depicted in the image below.

Image source original

How to choose the value of “K” in K-means clustering?

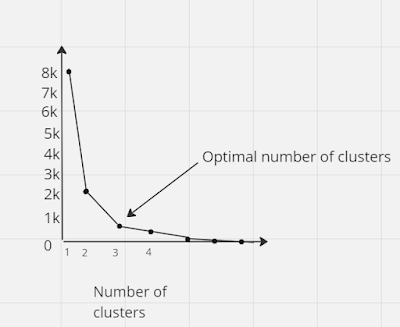
Identifying the ideal number of clusters is crucial for the effectiveness of the k-means clustering algorithm. The "Elbow Method" is a widely used technique for determining this value, relying on the concept of WCSS, or "Within Cluster Sum of Squares." This metric quantifies the total variability within each cluster. To calculate the WCSS value, the following formula is utilized

In the above formula of WCSS

: it is the sum of the square of the distance between each data point and its centroid with cluster 1 and for same goes for the other two terms.

The distance between the core and the points of data can be calculated using a variety of methods, such as the Manhattan and Euclidean distances. These distance measurements are meant to determine the degree of similarity or closeness between every cluster point of data and the center of the cluster.

To determine the optimal number of clusters using the elbow method, the following steps are typically followed:

• The elbow strategy in the K-means clustering algorithm involves applying several values of K, typically ranging from 1 to 10, to a dataset.
• For each value of K that may exist, the WCSS value needs to be ascertained.
• Plotting a curve using the computed WCSS values and the cluster count K comes next after the WCSS has been calculated.
• The curve mimics a human hum at the point where it meets the plot, which is the ideal value of K.

Image source original

Advantages of K-Means Clustering

• Simplicity: it’s easy to implement and understand, making it a popular choice for clustering tasks.
• Scalability: works well with large datasets and is computationally efficient, making it suitable for big data applications.
• Versatility: can handle different types of data and can be adapted for various domains, from customer segmentation to image processing.
• Speed: typically converges quickly, especially with large numbers of variables, making it efficient for many practical applications.
• Flexibility: allows the user to define the number of clusters (k), providing flexibility in exploring different cluster configurations.
• Initialization methods: offers multiple initialization methods to start the algorithm, reducing the sensitivity to initial seed points.
• Interpretability: provides straightforward interpretation of results, as each data point is assigned to a specific cluster.
• Robustness: can handle noisy and missing data reasonably well due to its cluster assignment approach.
• Efficiency with spherical clusters: works effectively when clusters are spherical or close to spherical in shape.
• Foundational algorithm: serves as a foundational clustering method, upon which various modifications and improvements, like K-medoids or fuzzy clustering, have been developed.

Disadvantages of K-means Clustering

• Centroids are placed sensitively in the clustering process, hence even little changes in their starting locations might lead to different clustering results in the end.
• The number of clusters (k) the user specifies determines the clustering result; this quantity may not always be known in advance and can have a big impact on the outcomes.
• Assumption of spherical cluster: works best when clusters are roughly spherical. It struggles with clusters of irregular shapes or varying densities.
• Vulnerable to outliers: outliers can substantially affect centroid placement, leading to potentially skewed clusters.
• Fixed cluster boundaries: hard assignment of data points to clusters can result in misclassification, especially at the boundaries between clusters.
• K-means clustering is sensitive to feature sizes; higher scale features may influence the grouping process more than smaller ones.
• Restricted to Euclidean distance: mostly depends on this metric, which could not work well with all kinds of data or domains.
• Not suitable for non-linear data – struggles to capture complex, non-linear relationships in data.
• Difficulty with clusters of varying sizes and densities: may not perform well with clusters that have significantly different sizes or densities.
• Convergence to local optima: the algorithm can converge to a local minimum, leading to suboptimal clustering solutions, especially in complex datasets.

Summary

K-means clustering is an easy and fast way to divide a dataset into "k" separate groups for unsupervised learning. In this method, data points are first assigned to the closest cluster center (or centroids) and then, until convergence is achieved, the centroids are constantly updated using the average of those points. K-means has a few disadvantages, such as the fact that it is prone to initial centroids selection, assumes spherical and equal-sized clusters, and is computationally efficient but requires a set number of clusters. Anomaly detection using k means clustering can also achieved.

Python Code

here is the k-means clustering Python code: - 

RANDOM FOREST IN MACHINE LEARNING/PYTHON/ARTIFICIAL INTELLIGENCE

Random Forest

• Types of Ensemble Methods
• Assumptions of Random Forest
• Advantages of Random Forest
• Random Forest Algorithm Working
• Applications of Random Forest
• Random Forest Regression
• Advantages of Random Forest Regression
• Disadvantages of Random Forest Regression

Random forest stands as a well-known supervised machine learning algorithm that can address both classification and regression problems within ML. Operating on ensemble learning principles, it leverages the collective intelligence of multiple classifiers to tackle intricate problems. This method harnesses the strengths of various models, improving the overall performance of the learning system. In this blog, we learn about random forest algorithms.

By amalgamating predictions from multiple decision trees, the random forest algorithm effectively mitigates overfitting while enhancing accuracy. Individual decision trees inherently possess high variance. However, when these trees are integrated into a random forest machine-learning model in parallel, the resulting variance diminishes. This reduction occurs because each decision tree is trained on a specific sample of data, ensuring that the output relies not on a single tree but on multiple trees, thereby lowering the overall variance.

In random forest models, higher numbers of trees correspond to increased accuracy while concurrently preventing overfitting tendencies, establishing a robust and more reliable model.

Image source original

Real-World Example for Random Forest

Let’s suppose we go for a hiking trip and get lost in the dense forest. Now we need to identify the type of tree we are under to navigate back to safety. But we find there are so many different trees, in such cases Random Forest, can help us it works like a team of expert tree guides that can help us to go back to safety.

A random forest isn’t a single decision tree, but it is a collection of trees, like a whole forest of knowledge. In random forests each tree votes for the type of tree it thinks it is. The final classification is based on the majority vote – the most popular choice among the trees.

When a new tree (data point) comes along, it’s passed through each decision tree in the forest. Each tree then votes for the type of tree it thinks the current tree is. The final classification is based on the majority vote – the most popular choice among the trees.

The advantage of using this method is that if one tree gets confused by an oddity, the others can compensate. Let’s take an example that one tree predicts that the current tree has bumpy bark, and it gets fooled, but other trees also have diverse knowledge that can classify the current tree correctly based on other features.

Random Forest’s strength lies in its multitude of perspectives. It’s like having many experts and each expert has their way of analyzing the data. They collaborate to make a more robust and accurate prediction, just like you’d be more confident in our hike if multiple guides agreed on the type of tree.

Types of Ensemble Methods

There are many verity of ensemble learning methods; they are:

Bagging (Bootstrap Aggregating) – In this approach, training involves using multiple models on randomly selected subsets of the training data. Following this, predictions from each model are aggregated, typically through averaging.

Boosting – This technique works in a sequence similar to a series of models, where training occurs one after the other, with each subsequent model dealing with the errors of the previous one. In this method, forecasts are combined through a weighted voting system.

Stacking – In this approach, the output from one model serves as input features for another model. Ultimately, the final prediction is derived from the second-level model.

Assumptions of Random Forest

Several decision trees are combined by a random forest technique to jointly forecast a dataset's class. Although individual trees in a forest may make incorrect predictions, the ensemble method ensures that most trees make accurate predictions. Let us now examine the two main assumptions behind the Random Forest classifier:

• For the Random Forest classifier in machine learning to make accurate predictions, it requires genuine values within the feature variables of the dataset rather than arbitrary or guessed values.
• Only when there is little to no correlation between the predictions given by the various trees can the Random Forest classifier perform successfully.

Why should we use Random Forest?

Below are some reasons or points that explain why we should use the Random Forest algorithm in machine learning:

• It takes a little amount of time to train when compared to rest algorithms.
• Its accuracy for prediction is high, and also with big datasets, it runs more efficiently.
• Furthermore, the Random Forest classifier can sustain its accuracy even in scenarios where a substantial part of the data is missing.

Random Forest Algorithm working

The two main random forest operations are the building phase and the prediction phase. During the construction phase, the algorithm builds a large number of decision trees, typically expressed as N trees. Random selections are made from a portion of the training data and feature set to create each decision tree. During the prediction stage, the algorithm generates predictions for every data point by utilizing the group of decision trees that were built during the first phase. Typically, before making a final prediction, all of the trees' projections are averaged or voted on. This rigorous process ensures that the random forest model can generate trustworthy predictions and resist variations in datasets.

First Step: Choose K randomly chosen data points from the training set to get started.

Second Step: Using the selected data subsets, decision trees are constructed in the second stage.

Third Step:  choose the number of decision trees (N) that you want to construct.

Fourth Step: Then, carry out steps 1 and 2 one more time.

Fifth Step: Get the projections from each decision tree and place the new data points in the most well-liked category.

To understand the working algorithm much better let’s look at one example.

Consider a dataset that contains several images depicting different fruits. These images are used as input for a machine-learning model that is constructed using a random forest classification technique. Using this strategy, the dataset is divided into smaller chunks, each of which is subjected to independent decision trees for analysis. Every decision tree generates a forecast when it is trained. When further data is added to the model, the Random Forest classifier predicts the result based on the output of the majority of the decision trees. This is an example of how this algorithm works.

Image source original

Applications of Random Forest

Let’s look at some applications of random forest where it is mostly used:

• Banking – it is used in the banking sector very much especially in the section of loan to check and identify the risk associated with it.
• Medicine – Using this algorithm, it becomes possible to discern disease patterns and assess the associated risks.
• Land Use – with the help of this algorithm we can identify the areas which have similar land.
• Marking – marking trends can be identified using this algorithm.
• Predicting continuous numerical values – This method can be employed to forecast various numerical outcomes such as housing prices, stock values, or the lifetime value of customers.
• Identifying risk factors – Additionally, it can identify risk factors for diseases, financial downturns, or other adverse occurrences.
• Handling high-dimensional data – because it uses decision trees inside it, therefore, it can analyze datasets that have quite a large number of features as input.
• Capturing complex relationships – Moreover, it can capture intricate connections between input features and target variables, enabling the modeling of complex relationships within the data.

What is Random Forest Regression?

Using ensemble techniques, random forest regression is one machine learning technique that combines regression and classification. Several decision trees and a procedure called Bootstrap Aggregation, or "bagging," are used in this strategy. Rather than depending just on one decision tree, a random forest combines several of them to produce the desired result.

An essential aspect of random forests is their utilization of multiple decision trees, each serving as an independent learning model. Through the Bootstrap method, sample datasets are generated for each model by randomly selecting rows and features from the original dataset. Predicting outcomes using Random Forest regression entails following standard procedures akin to other machine learning methodologies.

• Initially, we must formulate a precise question or specify the required data and identify the source from which to obtain the necessary data.
• We need to convert the data into an accessible format if it is not. 
• It's essential to identify and document all noticeable anomalies and missing data points within the dataset, as addressing these issues may be crucial for data quality and analysis purposes.
• Now we need to create a machine-learning model.
• For machine learning to work properly we need to establish a baseline model that we want to achieve.
• Following the data preprocessing steps, the next phase involves training the machine learning model using the prepared dataset.
• After training is done, we need to check its performance in unseen data or test data.
• Subsequently, it's essential to assess and compare the performance metrics between the test data and the model's predicted data.
• If the model’s performance does not achieve our expectations, we can try to improve it using tuning the hyperparameters or modeling the data with other techniques.
• At last, we interpret the data we have gained and report accordingly.

Out-of-bag score in Random Forest

The Out-of-Bag (OOB) score, also known as the Bag score, serves as a validation technique predominantly employed in bagging algorithms to assess their performance. This method involves extracting a small portion of validation data from the main dataset. Predictions are made on this specific validation subset, and the outcomes are subsequently compared with other results.

One significant benefit of the Out-of-Bag (OOB) score is its ability to evaluate the bagging algorithm's performance without using separate validation data. As a result, the OOB score provides an accurate assessment of the bagging algorithm's genuine performance.

To calculate the Out-of-Bag (OOB) score for a specific Random Forest algorithm, it is very important to set the OOB_Score parameter to "True" in the algorithm settings. This allows the algorithm to efficiently calculate and use OOB scores to evaluate its performance.

Advantages of Random Forest Regression

• We can easily use and it is less prone to be sensitive towards the training dataset compared to the decision tree.  
• It is more accurate as compared to a decision tree because it uses multiple decision trees inside it.
• It can easily handle large and complex datasets which have far more features.
• It can also easily tackle missing data problems, outliers’ detection, and noisy features.

Disadvantages of Random Forest Regression

• It can be not easy to understand.
• Subject matter experts may need to be involved for the Random Forest approach to be implemented successfully. They are essential for selecting and modifying parameters such as the number of decision trees, the maximum depth per tree, and the number of features to be taken into account at each split. A few key choices must be made to optimize the algorithm's performance and ensure accurate forecasts.
• Processing large datasets can be computationally costly.
• Overfitting can be a concern for Random Forest models when they become overly complex or contain an excessive number of decision trees. As a result, the model can perform poorly on fresh, untested data and overfit the training set.

Summary

Random Forest regression emerges as a robust solution for both continuous and classification prediction tasks, offering distinct advantages over traditional decision trees. Its ability to manage high-dimensional data, capture intricate relationships, and mitigate overfitting has propelled its widespread adoption across various domains and applications. Within a Random Forest, each constituent tree contributes its "vote" towards determining the most prevalent class in classification tasks or providing a prediction in regression scenarios. However, there's a risk of overfitting when employing excessively deep Random Forests or dealing with large and intricate datasets. Additionally, compared to individual decision trees, algorithms for Random Forest may exhibit lower interpretability due to their ensemble nature.

Python Code

here is the random forest Python example code: -