K-MEANS CLUSTERING IN MACHINE LEARNING/PYTHON/ARTIFICIAL INTELLIGENCE
K-means Clustering
- Unsupervised Machine Learning
- K-Means Algorithm Working
- Choosing the Value of "K" in K-Means
- Advantages of K-Means Clustering
- Disadvantages of K-Means Clustering
Unsupervised machine learning is the autonomous pattern identification within unlabeled data by computers. This method avoids the machine learning using already labeled data. Its task is to organize
unstructured data, detecting patterns, relationships, and variations
independently. Various algorithms are employed for this purpose, with one such
algorithm being K-Means clustering in machine learning.
One kind of unsupervised learning approach called K-Means clustering is intended to divide unlabeled datasets into discrete clusters. 'K' is the number of clusters the method seeks to find. For example, setting K=2 results in two clusters,
while K=3 yields three clusters, and so on. Through iterative steps, the
algorithm assigns data points to K clusters based on their similarities,
ensuring each point belongs to a distinct cluster with similar characteristics. We apply k means clustering for customer segmentation because in customer segmentation using k means clustering, it becomes easier to work and understand.
As a centroid-oriented
method, K-Means assigns a centroid to each cluster to minimize the
total distance between data points and their corresponding clusters. An
unlabeled dataset is first split into K clusters according to how similar the
data points are to one another. Through iterative refinement, the algorithm
adjusts the centroids until optimal clusters are achieved, with the specified
value of K dictating the number of clusters formed.
Real-world example for k-means clustering
Let’s take a real-world
example, there is a farmer’s market. However, as the market grew, it became more
disorganized, making it difficult for vendors and customers to navigate. To
end this problem the mayor of the village takes help from a data scientist
Emily.
Emily started her work by
meticulously gathering data on the products sold at the market, noting down
details such as type, color, and price. After gaining these pieces of
information, she apply k-means clustering algorithm to group similar
products. Fruits, vegetables, grains, dairy products, and more began to form
distinct clusters, creating a structured organization within the market.
After the clusters were identified the Mayor and Emily collaborated to redesign the layout of the market. They arranged vendor stalls according to the clusters, creating designed zones for each product category. Signs and labels were added to guide customers, ensuring a seamless shopping experience. They also use k means clustering for customer segmentation.
The k-means clustering algorithm mainly does two tasks:
- The iterative process of K-Means involves determining the optimal number of centroids or K center points. Through this iterative approach, the algorithm refines the value of K by evaluating various cluster configurations until an optimal solution is found.
- The K-Means algorithm assigns each data point to the nearest centroid or k-center. This process results in the formation of clusters where data points that are closest to a particular centroid are grouped together.
- Initially, the K-Means algorithm randomly selects k points from the dataset, designating them as means or cluster centroids.
- Subsequently, each item in the dataset is assigned to the nearest mean, grouping them into clusters. Following this, the means' coordinates are updated to the averages of all items within their respective clusters.
- The process iterates for a specified number of iterations, continuously refining the clusters with each iteration until convergence is achieved. At the end of the iterations, the algorithm produces the final clusters based on the updated means and the assignment of data points to their nearest centroids.
In this scenario, the
term "points" representing means denotes the average value of the
items grouped within the clusters. There are various methods to initialize
these means. One method involves randomly selecting items from the dataset to
serve as initial means. Another approach is to randomly generate mean values
within the range of the dataset's boundaries as the starting points.
Here is the pseudocode of
the K-means clustering algorithm:
Initialize k means with
random values
- For a given number of iterations:
- Iterate through items:
- Find the mean closest to the item by calculating the Euclidean distance of the item with each of the means
- Assign item to mean
- Update mean by shifting it to the average of the items in that cluster
Let’s look at the steps
of the k-means algorithm in machine learning and in general
Step 1 – Determine the
appropriate value for K, which indicates the desired number of clusters to be
created.
Step 2 – Choose K random
points or centroids as the initial cluster centers, which may or may not be
selected from the input dataset.
Step 3 – Assign each data
point to the centroid that is closest to it, thereby grouping the points into K
predefined clusters.
Step 4 – Compute the
variance within each cluster and position a new centroid at the center of each
cluster based on the calculated variance.
Step 5 – Proceed to the third stage iteratively, assigning each data point, using the revised centroids, to the closest centroid of the matching cluster.
Step 6 – If throughout the iteration any data points are moved to other centroids, the algorithm goes back to step 4 to recalculate the centroids. In any other case, it goes on to the last phase.
Step 7 – After doing all of the above steps now we can
say that our model is ready.
We can easily write the above clustering algorithm in Python.
Let’s understand the
algorithm using images:
It is now necessary to designate each point on the scatter plot to its nearest centroid or K-point. The process involves using mathematical formulas to determine the separation between two spots, thus we must draw a median between their centroids. displayed in the picture below.
Following the
reassignment observed in the depicted image, the algorithm progresses back to
the step involving the determination of new centroids or K-points.
How to choose the value of “K”
in K-means clustering?
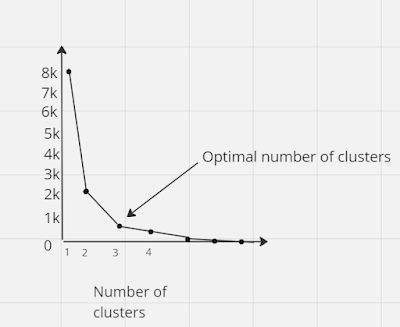
Identifying the ideal number of clusters is crucial for the
effectiveness of the k-means clustering algorithm. The "Elbow Method"
is a widely used technique for determining this value, relying on the concept
of WCSS, or "Within Cluster Sum of Squares." This metric quantifies
the total variability within each cluster. To calculate the WCSS value, the
following formula is utilized
In the above formula of
WCSS
: it is the sum of the
square of the distance between each data point and its centroid with cluster 1 and for same goes for the other two terms.The distance between
the core and the points of data can be calculated using a variety of methods,
such as the Manhattan and Euclidean distances. These distance measurements are
meant to determine the degree of similarity or closeness between every cluster
point of data and the center of the cluster.
To determine the optimal number of clusters using the elbow method, the following steps are typically followed:
- The elbow strategy in the K-means clustering algorithm involves applying several values of K, typically ranging from 1 to 10, to a dataset.
- For each value of K that may exist, the WCSS value needs to be ascertained.
- Plotting a curve using the computed WCSS values and the cluster count K comes next after the WCSS has been calculated.
- The curve mimics a human hum at the point where it meets the plot, which is the ideal value of K.
Advantages of K-Means Clustering
- Simplicity: it’s easy to implement and understand, making it a popular choice for clustering tasks.
- Scalability: works well with large datasets and is computationally efficient, making it suitable for big data applications.
- Versatility: can handle different types of data and can be adapted for various domains, from customer segmentation to image processing.
- Speed: typically converges quickly, especially with large numbers of variables, making it efficient for many practical applications.
- Flexibility: allows the user to define the number of clusters (k), providing flexibility in exploring different cluster configurations.
- Initialization methods: offers multiple initialization methods to start the algorithm, reducing the sensitivity to initial seed points.
- Interpretability: provides straightforward interpretation of results, as each data point is assigned to a specific cluster.
- Robustness: can handle noisy and missing data reasonably well due to its cluster assignment approach.
- Efficiency with spherical clusters: works effectively when clusters are spherical or close to spherical in shape.
- Foundational algorithm: serves as a foundational clustering method, upon which various modifications and improvements, like K-medoids or fuzzy clustering, have been developed.
Disadvantages of K-means Clustering
- Centroids are placed sensitively in the clustering process, hence even little changes in their starting locations might lead to different clustering results in the end.
- The number of clusters (k) the user specifies determines the clustering result; this quantity may not always be known in advance and can have a big impact on the outcomes.
- Assumption of spherical cluster: works best when clusters are roughly spherical. It struggles with clusters of irregular shapes or varying densities.
- Vulnerable to outliers: outliers can substantially affect centroid placement, leading to potentially skewed clusters.
- Fixed cluster boundaries: hard assignment of data points to clusters can result in misclassification, especially at the boundaries between clusters.
- K-means clustering is sensitive to feature sizes; higher scale features may influence the grouping process more than smaller ones.
- Restricted to Euclidean distance: mostly depends on this metric, which could not work well with all kinds of data or domains.
- Not suitable for non-linear data – struggles to capture complex, non-linear relationships in data.
- Difficulty with clusters of varying sizes and densities: may not perform well with clusters that have significantly different sizes or densities.
- Convergence to local optima: the algorithm can converge to a local minimum, leading to suboptimal clustering solutions, especially in complex datasets.
Summary
K-means clustering is an easy and fast way to divide a dataset into "k" separate groups for unsupervised learning. In this method, data points are first assigned to the closest cluster center (or centroids) and then, until convergence is achieved, the centroids are constantly updated using the average of those points. K-means has a few disadvantages, such as the fact that it is prone to initial centroids selection, assumes spherical and equal-sized clusters, and is computationally efficient but requires a set number of clusters. Anomaly detection using k means clustering can also achieved.
Python Code
Comments
Post a Comment